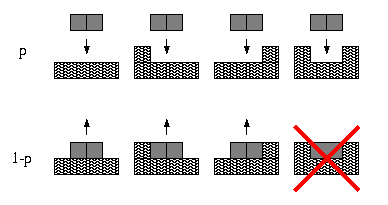
Surface growth studies
In Ref. [21]
we introduced a model for the growth of an interface by dimer
adsorption and desorption. Dimers (composite particles consisting of
two atoms) are adsorbed at sites of equal height at rate p and
evaporate at rate 1-p. The key feature of our model is that
evaporation is allowed only at the edges of terraces. In 1+1
dimensions the dynamic rules are:

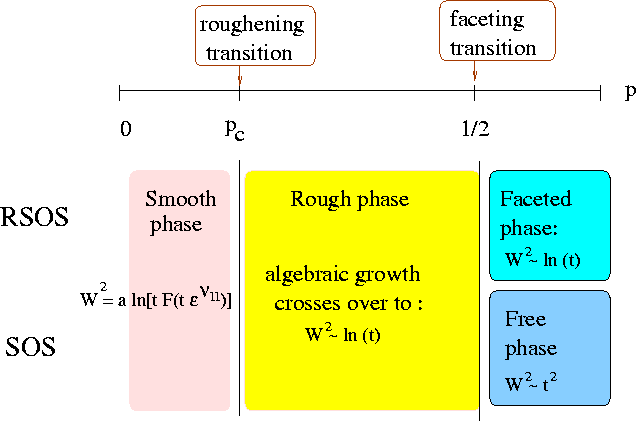
One of the most interesting properties of this model is a roughening transition from a smooth to a rough phase at the critical threshold p=0.3167. The following figure illustrates typical interface morphologies for various values of p:
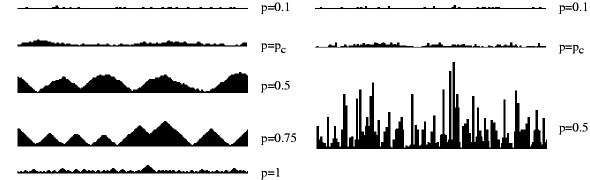
Restricted solid on solid (RSOS)
version
Unrestricted solid on solid (SOS) version
In the smooth phase, the interface selects spontaneously one height level as the bottom layer of the interface. The roughening transition is related to the so-called parity-conserving universality class (PC) which is represented most prominently by branching-annihilating random walks with two offspring A->3A, 2A->0. In such a process the particle density vanishes according to a power law with a certain critical exponent
n ~ (p-pc)0.92.
It can be shown that the density of exposed sites at the bottom
layer in our model vanishes with the same critical exponent, showing
that the roughening transition is closely related to the PC class. In
fact, the critical behavior at the first few layers may be explained
in terms of unidirectionally coupled PC processes:
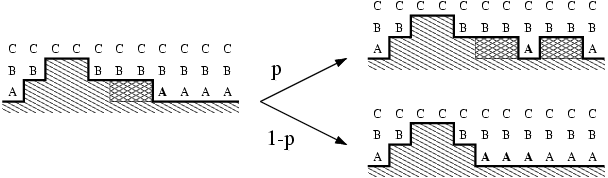
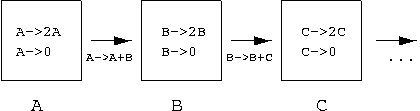
In Ref. [22] we explored the phase
structure of several variants (SOS, RSOS,random sequential, parallel
update) of this model in the p=(0,1) region and show that all
variants display the same type of universal critical behavior at the
roughening transition. Besides the roughening transition there is a
faceting transition as well at
the symmetry point of the model (p=1/2). The scaling properties are
insensitive on whether we use parallel or random sequential updates.
If we start the system from random initial distribution of hights
h=0,1
the dynamical properties will be different as the
consequence of
hard-core interactions.
Moreover, a parity conserving polynuclear
growth model is proposed that exhibits the same
critical behavior
at the roughening transition point as the dimer
model.
For more details see Ref. [52] ,
Talk at Rathen ,
[56]
or talk of IINM-2011 (Bhubaneswar, India)
arXiv:1109.2717.

Dec 18 2017