In this short introduction I present my primary field of interest through references of works I have been involved in. Of course these references do not form a complete bibliography of the field.
Continuous phase transitions in equilibrium statistical systems has been found to belong universality classes which are independent of the details of the interactions of finite range. Renormalization group (RG) method investigations has shown that they depend on the dimension and the symmetries of systems. Exact analytical treatment is not possible for most of the model systems investigated but approximate RG studies, numerical simulations have been used to explore the critical behavior (see Refs. [1,2,4,5]).
In non-equilibrium systems phase transition may occur as low as in one dimension since there are less interacting neighbors of variables and fluctuations can destroy ordered states. One might expect easier treatment of low dimensional models, but in fact it is hard to describe fluctuation dominated systems. Most methods start from fluctuation free, mean-field solutions (that is valid above a critical dimension) and add fluctuations perturbatively. The understanding of non-equilibrium phase transitions is incomplete as compared to equilibrium ones [42].
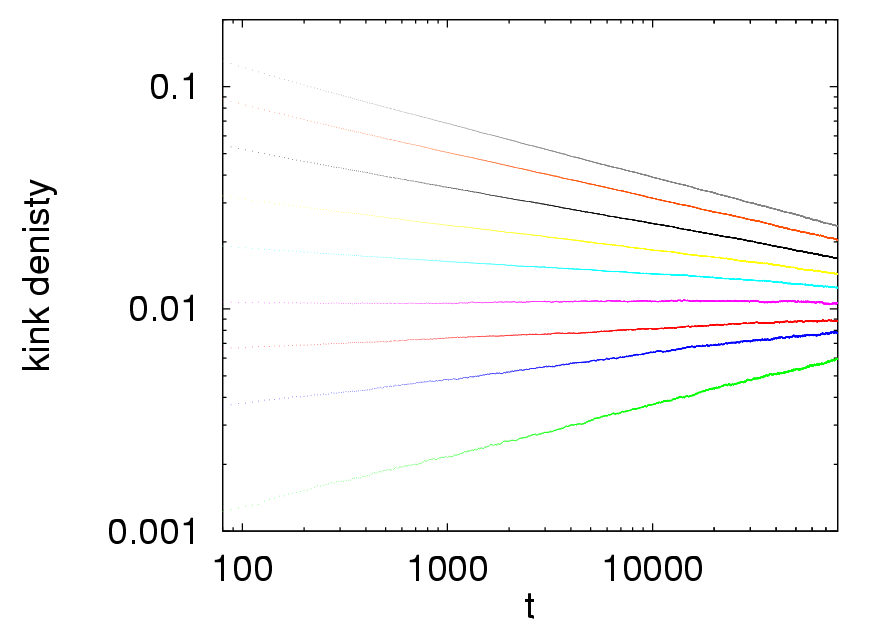
The dynamical critical behavior has been found to depend on initial conditions in many cases (see Refs. [19,20,22,24,25,28,27]). This means that it takes infinitely long time until the natural steady state correlations build up. This can happen when we introduce long-range initial correlations [19,24] or when we couple to another system that is either slowly varying [20,30] or creates blockades by hard-core interactions [22,25,28,27] between particles.

In the latter case the static exponents are effected as well and
new, robust universality classes emerge [28,27,34]
in one dimension that are insensitive to conservation laws that has been
found to be relevant in other non-equilibrium systems.
Such a conservation law is the parity of the number of particles that is responsible for the PC class in one-dimensional reaction diffusion models [13,15,16,17,18,24,45].
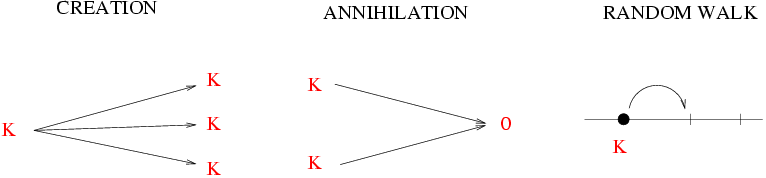
This kind of branching and annihilating random walks with two offspring's
(BAW2) arise in certain Ising systems (NEKIM) as kinks between ordered
domains as well, but here the Z2 symmetry
between the ordered, absorbing states is necessary condition too
[15,
17,
24,
35,
40]
for the appearance of the PC class.
At this critical behavior besides scaling a more general
local scale invariance (LSI)
of two-point, ageing functions seems
also be present asymptotically [48].
By destroying that symmetry either
by an external field [15]
or by fluctuations [17]
one obtains another robust class, the directed percolation class (DP).
The main representative model of this class is the branching and annihilating
random walk with one offspring (BAW1):
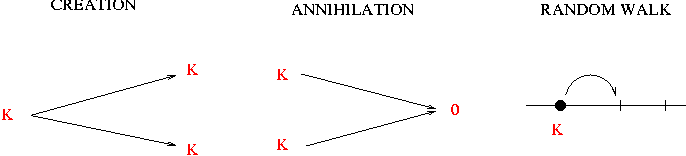
The DP class has been identified in many systems and according to
the hypothesis of Janssen and Grassberger all continuous phase transitions
to a single absorbing state in homogeneous systems with short ranged interactions
belong to this class provided there is no additional symmetry and quenched
randomness present. Unfortunately there have not been found too many experimental
realizations of this process yet, because any small imperfection causes
relevant perturbation and changes the scaling behavior.
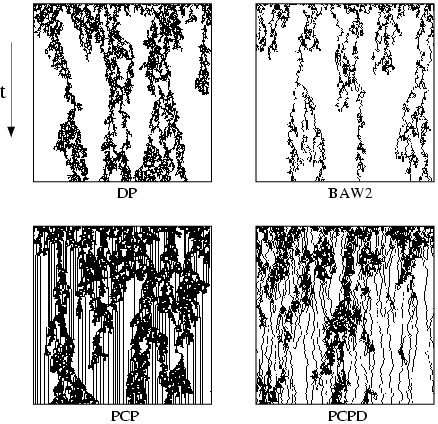 I have been involved
in the confirmation of this DP hypothesis for cellular automata type systems
using simulations and cluster mean-field approximations with coherent anomaly
extrapolation [9,
10,
11,
12,
31]
and could obtain estimates for the order parameter exponent with a few
percent accuracy.
I have been involved
in the confirmation of this DP hypothesis for cellular automata type systems
using simulations and cluster mean-field approximations with coherent anomaly
extrapolation [9,
10,
11,
12,
31]
and could obtain estimates for the order parameter exponent with a few
percent accuracy.
An interesting new class (PCPD) appearing in annihilation fission systems, where there are two absorbing states (one of them is fluctuating) without symmetry has just been investigated numerically [29, 26, 32, 33, 36, 39, 41,43]. Field theoretical description and understanding of the reasons of this class is still missing.
Recently reaction-diffusion models with production by triplets or quadruplets and explicit diffusion of particles have been found to exhibit novel types of critical behavior in low dimensions. Mean-field calculations and simulations in 1 and 2 dimansions were performed to determine the phase transition behavior of such general types of systems as well as the upper critical dimensions [38, 47].
The application of the basic absorbing state critical phenomena can be observed in SOC sandpile models or in certain surface growth models (see my page "Surface growth phenomena").
First order transitions have rarely been seen in one dimension [53]. There is a hypothesis from Hinrichsen, that they do not exists in one dimensional systems without extra symmetries, conservation laws or long range interactions. First order transitions have been found in the strong diffusion, mean-field like limit of the NEKIM model [13] and in case of the spin variables of the NEKIM model [17, 18] exhibiting Z_2 symmetry. In two dimensions hybrid triplet and quadruplet reaction-diffusion (RD) models [38] or the Ising model coupled to a quadruplet [RD] field [50] exhibit discontinuos transition for example. A combination of first and second order transition is the so-called mixed-order or hybrid phase transition. This means that at the transition point the order parameter exhibits a jump, in conjunction with a critical phenomena related to it. Examples for this occur in brain [90] and in fiber bundle [[100] models.
By going beyond the site mean-field approximation it turned out that the phase diagrams of reaction-diffusion models may contain other transition points with non-trivial scaling behavior. Cluster mean-field approximations and simulations in one and two dimensions showed that the diffusion plays an important role: it introduces a different critical point for strong couplings [44] besides those obtained by site mean-field solution at zero branching rate or by perturbative field theory. The non-trivial critical point, appearing by low diffusion rates exhibits the universal behavior of the transition of the 2A -> 3A, 2A -> 0 (PCPD) model owing to the generation of the effective 2A -> 0 reaction via the quick processes: 2A -> 3A -> 4A -> 0 [41,43].
Extensive simulations [46] suggest that PC class and more generally models with pair annihilation/coagulation reaction are a candidates for experimental observation. On the other hand spin-anisotropy, breaking the Z_2 symmetry can bring back DP type Griffiths phases as well as nonuniversal scaling [49]. Disorder can also be relevant in exclusion processes and lattice gases, causing different scaling behavior usually with slow dynamics [63].
It is known both for equilibrium and nonequilibrium systems that the presence of long-range interactions leads to different critical behavior compared to the universality classes characteristic for systems with short-range interactions. An alternative way of realizing long-range interactions is when the dynamical process is defined on a network with long links, which connect distant sites. These links can be fixed, i.e realize "quenched", long-range interactions. Networks can also be composed on top of d-dimensional regular lattices by additional long edges.
These arise e.g. in sociophysics , in fiber bundle models describing ruptures and damage in materials [84], [100] or in the context of conductive properties of linear polymers with crosslinks that connect remote monomers. Putting the contact process (A -> 2A, A -> 0) onto such networks we have provided numerical evidence that an absorbing phase transition occurs at some finite value of the infection rate and the corresponding dynamical critical exponents depend on the underlying network. Furthermore, the time dependent quantities exhibit log-periodic oscillations in agreement with the discrete scale invariance of the networks [54]. In case of random connections rare regions, non-universal scaling (Griffiths phase) and generic slow behavior may occur in these networks [57], [59],[62], [64],[67], [68],[69, [71],[72], [73][74], [77],[82], [85].
Heterogeneities also play an important role at network synchronization phenomena,
[87], which occur in brain models
[88],
[92], [93],
[94],
[98],
or in power-grids [83], [86].
Topological heterogeneity sometimes can be more relevant than interaction heterogeneity, altering the critical, universal
scaling behaior of the dynamical percolation of the Susceptible Infected Recovered epidemic model
[91].
For an overview of nonequilibrium universality classes see:
[42].
Nov 13, 2023.